Cours de Mathématiques en Cartes mentales

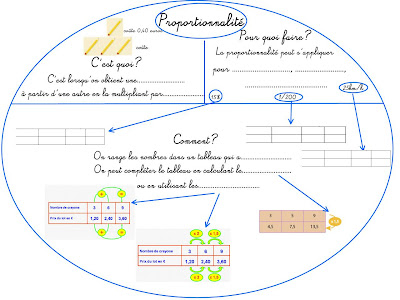
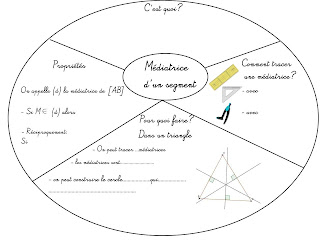
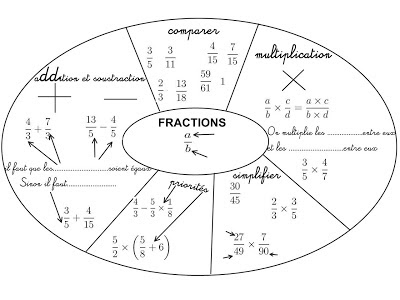
Mandala/ Schéma heuristique sur la trigonométrie - L'utilisation de la calculatrice est nécessaire, penser à appuyer sur la touche "seconde" ou "shift" pour faire l'inverse du cos, du sin ou de tan. - Le produit en c roix est à utiliser lorsque l'on calcule la longueur d'un c ôté pour cela considérer qu'il y a "1" en dessous de sin(35)

Définition d'une suite numérique, en particulier les suites arithmétiques et géométriques mais il en existe d'autres. Par exemple, pour la suite de Fibonacci donnée par Voici une très belle vidéo qui fait le lien avec la nature qui nous entoure avec le fameux nombre d'or  et encore http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/nature_dor.htm

Mandala-Carte mentale Parallélogrammes Vous trouverez ici les propriétés qui rassemblent le quadrilatère avec le parallélogramme, le rectangle, le losange et le carré. Ces propriétés étudiées en cinquième sont très utiles pour les démonstrations en quatrième. ⏯ NOUVEAU!! Vidéo avec commentaires!  👇 VERSION COMPL ÈTE Vocabulaire à connaitre:    diagonale, côtés consécutifs (qui se suivent), deux à deux (deux couples de côtés opposés) Du quadrilatère au parallélogramme il y a 2 "chemins": - s'il a ses côtés opposés parallèles 2 à 2 - s'il a ses diagonales qui se coupent en leur milieu Du quadrilatère au rectangle: - s'il a 3 angles droits Du quadrilatère au losange: - s'il a 4 côtés égaux Du parallélogramme au losange: - s'il a ses diagonales perpendiculaires - s'il a deux côtés consécutifs égaux Du parallélogramme au rectangle: - s'il possède un angle droit - si ses diagonales

Mandala Arithmétique: PGCD de deux nombres Remarques: - lorsque le PGCD de deux nombres vaut 1 cela signifie que ces deux nombres sont "premiers entre eux": La seule fois où on les trouve dans une même table c'est la table de 1 qui contient tous les nombres entiers. - Une fraction dont le numérateur et le dénominateur sont premiers entre eux est déjà irréductible (on ne peut plus la simplifier) - Chaque nombre a au moins deux diviseurs: 1 et lui même Pour les problèmes: Puisque PGCD (32, 12) = 4 ( garder en tête qu'un PGC D sert à D iviser) - concernant les gommes et les stylos ont peut faire 4 paquets identiques, dans chaque paquet il y aura:    32 : 4 = 8 stylos                                    12 : 4 = 3 gommes - concernant le rectangle à partager chaque carreau va mesurer 4 cm de côté ( 32 et 12 sont des centimètres, donc le PGCD aussi est en centimètres) On peut trouver le nombre de carreaux nécessaires pour recouvrir ce rectang

Mandala "Distance d'un point à une droite" - Dans c'est quoi?: Le nageur fait référence à la découverte intuitive: quel est le trajet le moins fatigant à emprunter pour rejoindre la rive? - Dans comment?: rappel de l'importance de l'angle droit - Dans autre distance: celle d'un point à un autre mais qui n'est pas vraie en  dimension (exemple d'un vol Paris New York où l'avion ne va pas "en ligne droite" mais se rapproche du pôle Nord pour une distance moindre" La notion de bissectrice qui est aussi rattachée à la distance d'un point à une droite sera traité à part

Les entiers naturels sont ceux qui sont positifs. Les nombres rationnels sont ceux qui peuvent s'écrire sous la forme d'une fraction. Tous les entiers sont décimaux et rationnels ( 5 = 5,0 = 5/1) mais la réciproque est fausse. Tous les décimaux sont rationnels ( 3,2  = 32/10 ) mais la réciproque est fausse  (1/3 = 0,3333.... n'est pas décimal car il y a une infinité de chiffres) . Les irrationnels ne peuvent pas s'écrire sous forme de fraction .

Très beau schéma heuristique tiré du site http://www.stylo-rouge-et-crayon-gris.fr/ que je mets en favori!

Une fiche type  "mandala" à adapter pour vous aider à réviser, si vous n'avez pas beaucoup de temps cibler d'abord les chapitres qui vous posent le plus de problèmes. Comment s'y prendre? Lire et relire la leçon puis compléter chaque partie. Ci-dessous un document vide que vous pouvez imprimer.

Mandala Equations du premier degré à une inconnue

Mandala Cosinus d'un angle aigu dans un triangle rectangle -Formule qui fait le lien entre angles et longueurs - Le rapport côté adjacent à l'angle/ hypoténuse est toujours le même lorsque l'angle est le même - le cosinus ne dépend pas de la taille du triangle - le cosinus permet de calculer la longueur d'un côté inconnu ou alors de calculer la mesure d'un angle inconnu

Mandala Proportionnalité La représentation graphique est une droite passant par l'origine

Mandala Théorème de Thalès -Dans "C'est quoi?": La pyramide, l'astronome qui tombe dans le puits et l'âne chargé font références aux anecdotes de la vie de Thalès . -Dans "Pourquoi?": importance du parallélisme qui entraine la proportionnalité des dimensions entre les deux triangles - Dans "Comment?": on repère les droites parallèles mais aussi le point "important"(ici T) qui n'est pas contenu dans les droites parallèles, ce point constitue le point de départ, pour finir on utilise le produit en croix.

Mandalas calculs de nombres relatifs Addition et soustraction - pour les addition les deux cas sont: termes de même signe ou de signes opposés - on peut supprimer les parenthèses et les signes "+" inutiles (pas le "+" de l'addition!) - soustraire un nombre revient à additionner son opposé - pour mener le calcul A: d'abord changer les soustractions en addition, puis regrouper les termes de même signe et enfin calculer NOUVEAU: Vidéo explicative + carte mentale complète

Mandalas Puissances de 10 Les espaces sont consacrés aux exemples 1<=a<10 Une vidéo courte pour prendre conscience de de l'infiniment grand à l'infiniment petit en 44 images 

Mandala "Nombres relatifs" NOUVEAU Vidéo explicative et version complète

 Mandala "Puissances" Mots manquants: facteur, exposant, négatif, positif, pair, impair. Remarque: Pour déterminer le signe de On applique la règle des trois "p " : p arenthèses et exposant p air donnent un résultat p ositif NOUVEAU : vidéo explicative  + carte mentale complète

Mandala "Somme des angles d'un triangle" Avant de coller le triangle il faut colorier chacun des trois angles d'une couleur différente, au recto et au verso, cela permet de se rendre compte que l'association des trois angles donne un angle plat (180°) en faisant un pliage selon les pointillés . A compléter: - la valeur de chaque angle pour le triangle équilatéral - l'égalité des angles à la base pour le triangle isocèle - les deux angles aigus sont complémentaires pour le triangle rectangle NOUVEAU: Explication vidéo + version complète:

Mandala "Fractions" pour quatrièmes et troisièmes Version élèves                                             Version complète                                                        Nouveau! Vidéo explicative

Mandala "Proportionnalité" Mots manquants : grandeurs, même coefficient, pourcentage, échelle, vitesse, deux lignes coefficient, colonnes

Mandalas "Triangles rectangles et cercles" En Allemagne cette propriété est appelé "Théorème de Pythagore"

  Mandala  " M édiatrices "

Mandala "Fractions " Pour l'addition la taille des deux lettres "d" n'est pas une faute de frappe mais une allusion à "deux fois le même dénominateur"

Mandala"Calcul littéral" La parenthèse est matérialisée par la trousse, objet bien connu des élèves! Remerciements à Daniel Mentrard pour l’emprunt d'images provenant de son excellent site: dmentrard.free.fr

Mandala  "Calculs de nombres relatifs: les quatre opérations" Pour la règle des signes pour les produits et quotients il est fait allusion à "l'ami de mes amis est mon ami et l'ennemi de mes ennemis est mon ami" Pour l'addition les deux cas "pour le même signe" et "pour les signes opposés" sont représentés par "chien" et "chat"

Mandala"Réciproque du théorème de Pythagore" ⏯NOUVEAU! Vidéo commentée 👇 VERSION COMPL ÈTE

Mandala "Théorème de Pythagore" NOUVEAU Carte mentale complète + vidéo explicative

Mandala"Inégalité triangulaire"

Mandala "Règles de calcul et priorité"

Mandala "Symétrie centrale"